In this video series, we will show you the most common variants of the planar four-bar linkage, as well as their characteristics and special features. These variants can be derived from the theorem of Grashof.
Grashof’s condition for four-bar linkages states: The shortest link of a four-bar linkage can fully rotate in relation to its neighbouring links, if the sum of the lengths of the shortest and longest link is smaller – or at least equal, in the limit case – than the sum of the other two link lengths. The longest link in the four-bar linkage can be a neighbouring link of the shortest link or it can be situated opposite to it.
According to the usual conventions for four-bar linkages, we name the links and joints as follows: The shortest link is always designated a, the remaining links are designated b, c and d in a clockwise direction.
For joints, the following applies, analogously: Joint 1 is between a and d and from there the further numbering up to 4 is also done clockwise.
Alternatively, the fixed link is usually referred to as the frame and the link opposite from it as the coupler. The other two links are often called grounded links.
By deciding which of the links b, c and d is the longest, as well as by different choices for the frame, different types of four-bar linkages can then be derived.
We continue our video series with the double-crank. It is mainly used in manufacturing and agricultural machinery. In contrast to the crank-rocker, both b and d can rotate fully here (two cranks), which is where its name comes from.
As with the crank-rocker, the following conditions must also be fulfilled according to Grashof: a+b < c+d, a+c < b+d or a+d < b+c. The difference to the crank-rocker is the choice of the frame, and from the crank-rocker we already know that a can rotate fully, relative to its neighbouring links. If we now choose a as the frame, both its neighbours become cranks. The link c can perform a full rotation relative to the frame during one cycle of the motion, but it can only swing back and forth within a limited range of angles relative to its neighbours b and d.
Here, the lengths a to d were chosen as follows:
a = 76 (min), b = 191, c = 124, d = 219 (max)
Thus, the following applies: a+d = 76+219 = 295 < 315 = 191+124 = b+c
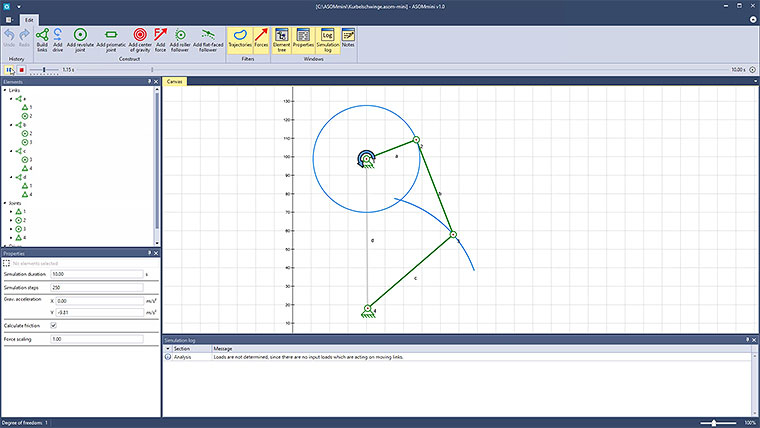
In ASOMmini, such linkages can be designed, simulated and analyzed kinematically very quickly and easily. They can also be modified and optimized in real time. The same also applies for more complex kinematic systems, which can also be implemented without difficulty using our software.