In dieser Videoreihe zeigen wir Ihnen die bekanntesten Varianten des planaren Viergelenks, sowie deren Eigenschaften und Besonderheiten. Diese Varianten lassen sich aus dem Satz von Grashof ableiten.
Die Grashof‘sche Bedingung für Viergelenke besagt: Das kürzeste Glied einer Viergelenkkette ist gegenüber seinen Nachbargliedern voll umlauffähig, wenn die Summe der Gliederlängen des kürzesten und längsten Gliedes kleiner ist – oder im Grenzfall gleich – als die Summe der beiden anderen Gliederlängen. Dabei kann das längste Glied im Gelenkviereck ein Nachbarglied des kürzesten sein oder diesem gegenüber liegen.
Nach den üblichen Konventionen für Viergelenke benennen wir die Glieder und Gelenke wie folgt: Das kürzeste Glied trägt stets die Bezeichnung a, die restlichen Glieder werden dem Uhrzeigersinn folgend mit b, c und d bezeichnet.
Für Gelenke gilt analog: Gelenk 1 liegt zwischen a und d und von dort erfolgt die weitere Nummerierung bis 4 ebenfalls im Uhrzeigersinn.
Alternativ wird das feststehende Glied üblicherweise auch als Gestell und das ihm gegenüberliegende Glied als Koppel bezeichnet. Die beiden restlichen Glieder heißen in diesem Zusammenhang Lenker.
Durch die Entscheidung, welches der Glieder b, c und d das längste ist, sowie durch unterschiedliche Wahl des Gestells, können dann verschiedene Viergelenktypen erzeugt werden.
Betrachten wir nun die oben genannten Grenzfälle der Grashof´schen Ungleichung. Das sind jene Fälle, bei denen es mindestens zwei kürzeste und mindestens zwei längste Glieder gibt, woraus folgt, dass die Summe des kürzesten Gliedes und des längsten Gliedes nun genau gleich der Summe der übrigen Glieder sein muss. Damit wird die Ungleichung zu einer Gleichung.
Für die Anordnung der Gliederpaare sind nun folgende Unterscheidungen denkbar:
- Gliederpaare mit gleichen Längen liegen sich gegenüber (Parallelogramm).
- Gliederpaare mit gleichen Längen liegen nebeneinander (Deltoid).
- Alle 4 Glieder sind gleich lang (Quadrat/Raute).
Für alle diese Fälle (mit Ausnahme des zweiten) gilt, dass unabhängig von der Gestellwahl stets beide Lenker Kurbeln sind, ähnlich wie bei der Doppelkurbel.
Im Bewegungsablauf all dieser Sonderfälle treten aber zusätzlich stets zwei zwanglose Lagen auf, in denen das Getriebe durchschlagen kann. Das heißt, dass alle Glieder in einem Moment aufeinander bzw. in einer Linie liegen, wodurch sich mehrere Lösungen für die Weiterführung der Bewegung aus einer solchen Lage heraus ergeben. Dies kann in der Praxis zu großen Problemen führen, vor allem beim Start aus einer solchen Position. Daher werden solche Getriebe meist nur im „sicheren“ Bereich genutzt, wo sie nicht durchschlagen.
Im letzten Teil unserer Reihe sind noch die letzten beiden dieser Fälle zu betrachten.
Widmen wir uns zunächst dem zweiten Fall, bei dem gleichlange Glieder stets direkt benachbart sind. Hier kann man ebenfalls zwei Unterfälle ableiten, nämlich durch die Entscheidung, ob eines der kurzen oder eines der langen Glieder als Gestell gewählt wird.
So können durch die Wahl eines kurzen Gliedes als Gestell, wie im ersten Video gezeigt, die beiden benachbarten Glieder als Lenker relativ zum Gestell voll umlauffähig gemacht werden. Das Getriebe wird dann gleichschenklige Doppelkurbel genannt.
Hier wurden die Längen a bis d wie folgt gewählt:
a und d = 50 (min), b und c = 146 (max)
Damit gilt die Gleichung: a+b = 196 = c+d oder a+c = 196 = b+d
Wählt man hingegen ein langes Glied als Gestell, wie im zweiten Video gezeigt, erhält man die gleichschenklige Kurbelschwinge. Wie bei der einfachen Kurbelschwinge wird dabei der kurze Lenker zu einer Kurbel und der lange Lenker zu einer Schwinge.
Hier wurden die Längen a bis d wie folgt gewählt:
a und b = 100 (min), c und d = 158 (max)
Damit gilt die Gleichung: a+c =258 = b+d oder a+d = 258 = b+c
Beide Getriebe finden nur in speziellen Ausnahmen Anwendung, da sie, anders als ihre jeweiligen Namensvettern, durch das mögliche Durchschlagen Probleme bereiten können.
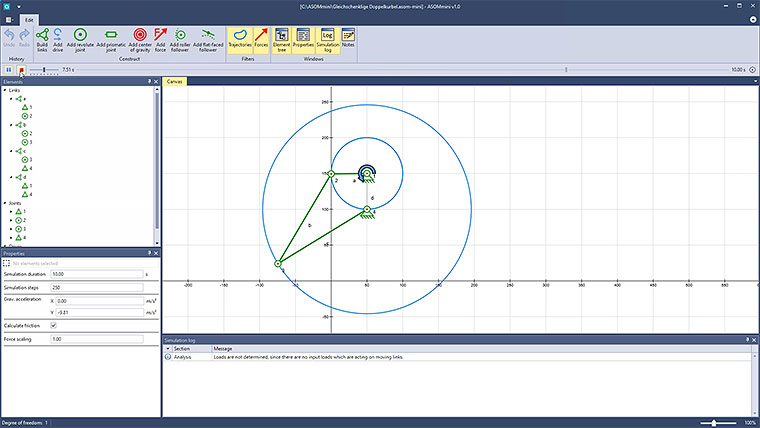
Der dritte Fall, der manchmal auch als Rauten– oder Rhombuskurbel bezeichnet wird, stellt seinerseits wiederum einen Sonderfall zu den ersten beiden Fällen dar, da nicht nur jeweils 2 Glieder gleichlang sind, sondern alle vier. Damit gilt, dass in den zwanglosen Lagen nicht nur die Glieder übereinander liegen, sondern dass zusätzlich auch noch die Gelenke paarweise übereinander liegen.
Simuliert man ein solches System, wie im dritten Video gezeigt, so muss man sich darüber im Klaren sein, dass in der Praxis schon durch leichte Abweichungen bei der Fertigung der Bauteile (die sich kaum vermeiden lassen) ein deutlich anderes Verhalten, sowohl in der Bewegung als auch bei der Kraftverteilung, entstehen kann.
Hier wurden die Längen a bis d wie folgt gewählt:
a, b, c und d = 150 (min und max)
Damit gilt die Gleichung: a+b = 300 = c+d oder a+c = 300 = b+d oder a+d = 300 = b+c
In ASOMmini lassen sich derartige Koppelgetriebe schnell und einfach konstruieren, simulieren und kinematisch analysieren, außerdem können sie auch in Echtzeit modifiziert und optimiert werden. Das gilt auch für komplexere Anordnungen, die sich mit unserer Software ebenfalls problemlos realisieren lassen.