In dieser Videoreihe zeigen wir Ihnen die bekanntesten Varianten des planaren Viergelenks, sowie deren Eigenschaften und Besonderheiten. Diese Varianten lassen sich aus dem Satz von Grashof ableiten.
Die Grashof‘sche Bedingung für Viergelenke besagt: Das kürzeste Glied einer Viergelenkkette ist gegenüber seinen Nachbargliedern voll umlauffähig, wenn die Summe der Gliederlängen des kürzesten und längsten Gliedes kleiner ist – oder im Grenzfall gleich – als die Summe der beiden anderen Gliederlängen. Dabei kann das längste Glied im Gelenkviereck ein Nachbarglied des kürzesten sein oder diesem gegenüber liegen.
Nach den üblichen Konventionen für Viergelenke benennen wir die Glieder und Gelenke wie folgt: Das kürzeste Glied trägt stets die Bezeichnung a, die restlichen Glieder werden dem Uhrzeigersinn folgend mit b, c und d bezeichnet.
Für Gelenke gilt analog: Gelenk 1 liegt zwischen a und d und von dort erfolgt die weitere Nummerierung bis 4 ebenfalls im Uhrzeigersinn.
Alternativ wird das feststehende Glied üblicherweise auch als Gestell und das ihm gegenüberliegende Glied als Koppel bezeichnet. Die beiden restlichen Glieder heißen in diesem Zusammenhang Lenker.
Durch die Entscheidung, welches der Glieder b, c und d das längste ist, sowie durch unterschiedliche Wahl des Gestells, können dann verschiedene Viergelenktypen erzeugt werden.
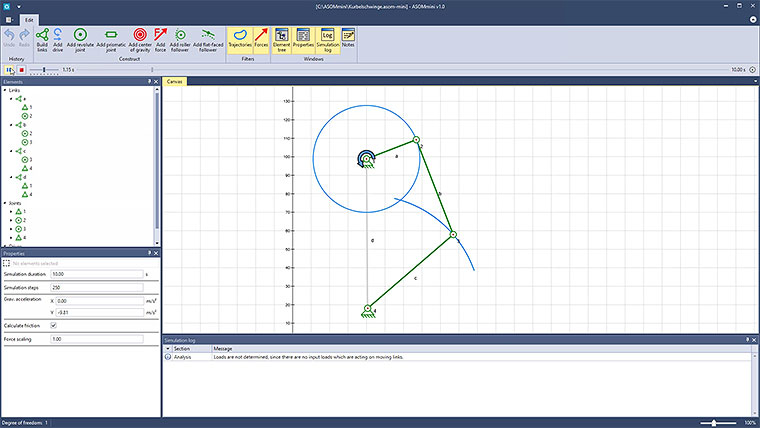
Den Start in unserer Videoreihe macht die Kurbelschwinge. Die Kurbelschwinge ist die wahrscheinlich am häufigsten verwendete Ausprägung der Viergelenkkette. Sie bezieht ihren Namen aus der Eigenschaft, dass ein Lenker eine volle Umdrehung ausführen kann (die Kurbel), während der andere nur einen begrenzten Winkelbereich überstreicht (die Schwinge).
Kurbelschwingen müssen also zum einen Viergelenke sein, die nach der Grashof’schen Regel umlauffähig sind. Damit gilt a+b < c+d, a+c < b+d oder a+d < b+c. Zusätzlich muss ein Nachbarglied von a, also b oder d, als Gestell gewählt werden, so dass a einer der Lenker wird und sich relativ zum Gestell (und der Koppel) vollständig drehen kann.
Hier wurden die Längen a bis d wie folgt gewählt:
a = 29 (min), b = 55, c = 61, d = 81 (max)
Damit gilt: a+d = 29+81 = 110 < 116 = 55+61 = b+c
Als Gestell wurde d gewählt. Damit ist das Beispiel definitiv eine Kurbelschwinge.
In ASOMmini lassen sich derartige Koppelgetriebe schnell und einfach konstruieren, simulieren und kinematisch analysieren, außerdem können sie auch in Echtzeit modifiziert und optimiert werden. Das gilt auch für komplexere Anordnungen, die sich mit unserer Software ebenfalls problemlos realisieren lassen.